黄瓜养殖基地！

《shader入门精要》笔记-第4章-数学基础

发表于 分类于

点和矢量

点积(内积)和叉积(外积)

内积

Shader代码中使用dot(a,b)来进行矢量的点积运算.

1
a·b = (a x , a y , a z ) ·(b x , b y , b z ) = a x b x  + a y b y  + a z b z

满足交换律和结合律.
使用:

  • 投影
    单位矢量a,和一个长度不限制的矢量b,dot(a,b)得到b在a方向上带有符号的投影

外积

外积的结果时矢量,并非标量.

1
a X b = (a x , a y , a z ) X (b x , b y , b z ) = (a y b z  - a z b y , a z b x  - a x b z , a x b y  - a y b x )

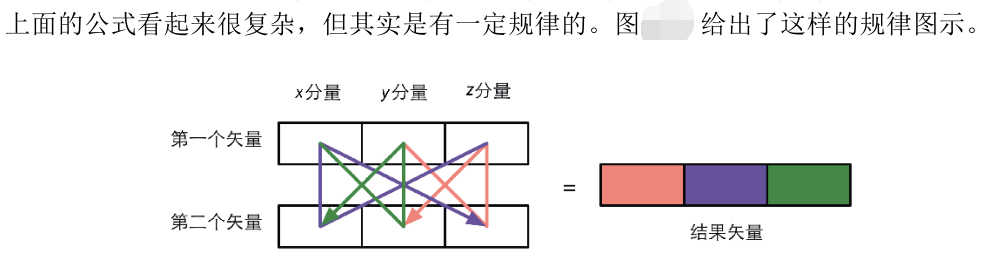
20190313215648.png
例如:
(1, 2, 3) X (−2, −1, 4) = ((2)(4) − (3)(−1), (3)(−2) − (1)(4), (1)(−1) − (2)(−2))
= (8 − (−3), (−6) − 4, (−1) − (−4)) = (11, −10, 3)
外积不满足交换律,即a X b不等于b X a.
然而外积满足反交换律,即a X b = -(b X a)
外积不满足结合律.

矩阵(matrix)

矩阵运算

矩阵乘法

  • 矩阵乘法不满足交换律
    AB不等于BA
  • 矩阵乘法满足结合律
    (AB)C = A(BC)

shader中主要使用4x4矩阵来运算.

特殊矩阵

方块矩阵(方阵)

行和列数目相等的矩阵.
三维渲染里,用的最多的是3x3和4x4的方阵

单位矩阵

用In来表示.比如I3是3x3的单位矩阵.

转置矩阵

transposed matrix
转置矩阵实际是对原矩阵的一种运算,即转置运算.给定一个rXc的矩阵M,他的转置可以表示为MT(T为上标)(辣鸡MD).数学公式是:
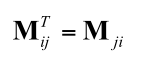
20190313221834.png
例如:
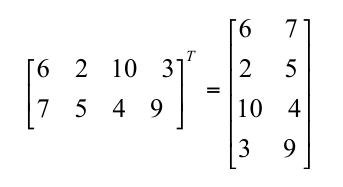
20190313221856.png

转置矩阵性质:
  • 转置矩阵的转置等于原矩阵(废话)
  • 矩阵的串接转置等于反向串接各个矩阵的转置
    即:
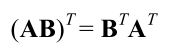
    20190313222114.png

逆矩阵

给定一个矩阵M,用M-1(-1为上标)表示M的逆矩阵.
MM-1为单位矩阵

矩阵可逆的条件:
  • 矩阵为方块矩阵
  • 矩阵的行列式不为零

虽说在学数学…但是也是shader开发里的数学…还是不去回忆具体怎么求逆矩阵了,交给程序去做=v=

逆矩阵的性质
  • 逆矩阵的逆矩阵等于原矩阵
  • 单位矩阵的逆矩阵是其本身
  • 转置矩阵的逆矩阵等于逆矩阵的转置
    即:
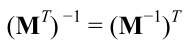
    20190313222923.png
  • 矩阵串接相乘后的逆矩阵等于反向串接各个矩阵的逆矩阵
    即:
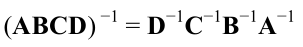
    20190313223054.png

正交矩阵

蒸饺正交是矩阵的一种属性.如果一个方阵M和它的转置矩阵的乘积是单位矩阵的话,我们说这个矩阵是正交的
即:
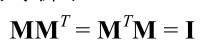
20190313223516.png

行矩阵or列矩阵?

书上p64
这里不说过程了.
结论是,unity中习惯把矢量转换成列矩阵,并放在矩阵的右侧进行计算.

矩阵的几何意义: 变换

变换的类型

线性变换

可以保留矢量加和标量乘的变换.用数学公式表达即是:
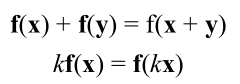
20190313225105.png
上面的式子很抽象.
缩放就是一种线性变换.如f(x) = 2x,可以表示一个大小为2的统一缩放.
旋转也是一种线性变换 对于线性变换来说,仅仅使用3X3矩阵可以表示三维坐标下的所有线性变换.
线性变换除了包括旋转和缩放外,还包括错切,镜像,正交投影等.

仿射变换

仅有线性变换是不够的,要考虑平移交换.如,f(x) = x + (1,0,0)这个变换就不是一个线性变换.
三维坐标下,我们不能用一个3x3的矩阵来表示一个平移变换.
这样,就有了仿射变换.
仿射变换是合并了线性变换和平移变换的变换类型.三维空间下的仿射变换可以用一个4x4的矩阵来表示.为此,我们需要把矢量扩展到四维空间下,这就是齐 次 坐 标 空 间(homogeneous space).
不知道是什么鸡儿玩意单好像以后有用的表
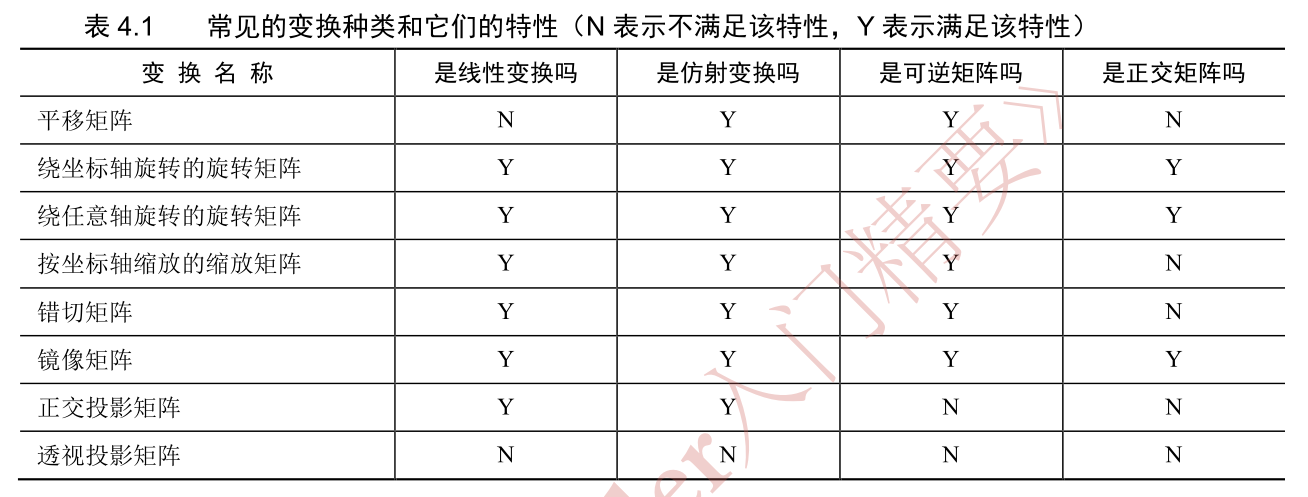
20190314081017.png

齐次坐标

因为3X3矩阵不能表示平移,所以我们用4x4矩阵.为此,我们还需要把原来的三维矢量转换成四维矢量,也就是齐次坐标(homogeneous coordinate).
对于一个点,从三维坐标转换为齐次坐标是将其w分量设为1,而对于方向矢量而言,需要把其w分量设为0.
这样的设置会导致,用一个4x4矩阵对一个点进行变换的时候,平移,缩放,旋转都会被施加于该点.但是如果用于变换一个方向矢量,平移的效果就会被忽略.

分解基础变换矩阵

我们可以把一个基础变换矩阵分解成4个组成部分.
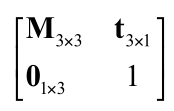
20190314081831.png
其中,左上角的M是一个用于旋转和缩放的三维矩阵.
t表示平移.
最后一行是固定的[0 0 0 1]

平移矩阵

M为单位矩阵时,整个4x4矩阵只代表平移.
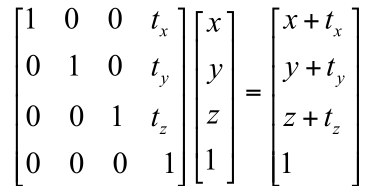
20190314082140.png
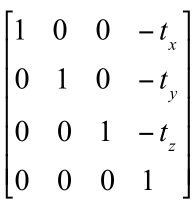
平移矩阵的逆矩阵就是反向平移的矩阵.
20190314082256.png

缩放矩阵

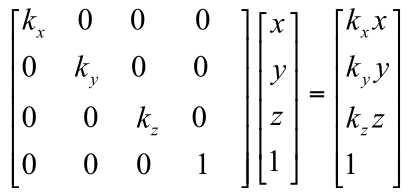
20190314082409.png
如果缩放系数kx = ky = kz,我们把这样的缩放称为统一缩放否则称为非统一缩放.
直观上看,统一缩放就是等比缩放模型,而非统一缩放会拉伸或挤压模型.
统一缩放不会改变角度和比例信息,非统一缩放会改变模型相关的角度和比例.
在进行法线变换时,如果存在非统一缩放,直接用于变换顶点的变换矩阵的话,就会得到错误的结果.(正确的方法见4.7节)

旋转矩阵

按x轴旋转:

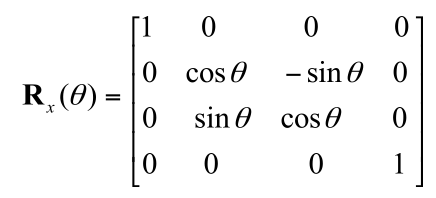
20190314084552.png

按y轴旋转

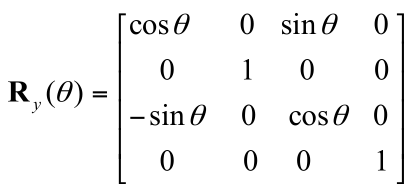
20190314084627.png

按z轴旋转

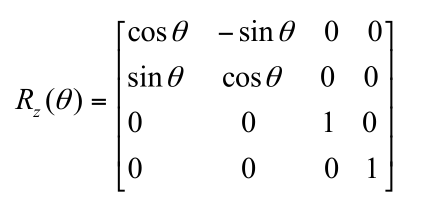
20190314084643.png

复合变换

我们可以把平移,旋转,缩放结合起来,组成一个复杂的变换过程.
例如,可以对一个模型先进行大小为(2, 2, 2)的缩放,再绕y轴旋转30度,最后向z轴平移4个单位.
复合矩阵可以通过矩阵的串联来实现.
如:
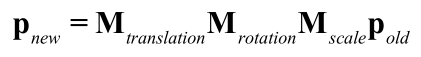
20190314085018.png
需要注意的是,因为矩阵的乘法不满足交换律,变换的结果是依赖于变换顺序的.
绝大多数情况下,我们约定变换的顺序是,先缩放,再旋转,最后平移.

坐标空间

模型空间

也称对象空间或局部空间.

世界空间

最外层的坐标空间

观察空间

也称为摄像机空间
Unity中观察空间的+x轴指右方,+y轴指向上方,+z轴指向摄像机的后方----Unity在模型空间和世界空间选用的是左手坐标系,而观察者空间选用右手坐标系.

观察空间和屏幕空间是不同的.观察空间是一个三维空间,而屏幕空间是一个二维空间.从观察空间到屏幕空间需要一个投影(projection)转换.

顶点变换的第二步,就是将顶点坐标从世界空间变换到观察空间.这个变换通常叫做观察变换.

剪裁空间

顶点接下来要从观察者空间转换到剪裁空间(clip space,也被称为齐次裁剪空间)中,这个用于变换的举证叫做裁剪矩阵(clip matrix),也被称为投影矩阵(projection matrix).
剪裁空间的目标是能够方便地对渲染图元进行裁剪.完全位于这块空间内部的图元将会被保留,完全处于这块空间外部的图元将会被剔除,而与这块空间边界相交的图元就会被裁剪.这块空间是由视锥体(view frustum)决定的.

视锥体指的是空间中的一块区域,这块区域决定了摄像机可以看到的空间.视锥体由留个平面包围而成,这些平面被称为裁剪平面(clip planes).
视锥体有两种类型,这涉及两种投影类型----一种是正交投影(orthographic projection),一种是透视投影(perspective projection)
20190317191236.png
透视投影会有远小近大.

在视锥体的6块裁剪平面中,有两块裁剪平面比较特殊,分别是近剪裁平面(near clip plane)和远剪裁平面(far clip plane).它们决定了摄像机可以看到的深度范围.
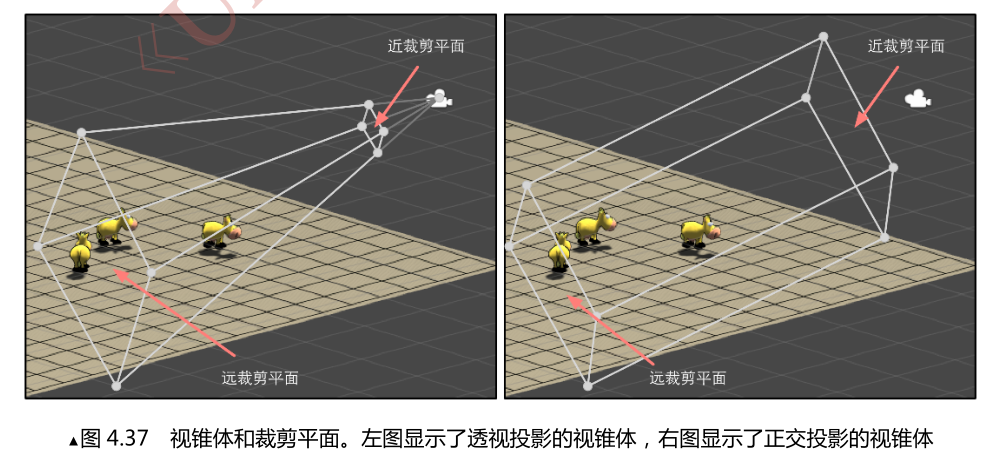
20190317191631.png
我们通过一种通用,简洁的方式进行剪裁工作,这种方式是通过一个投影矩阵把顶点转换到一个剪裁空间中.
投影矩阵有两个目的:

  • 首先是为投影做准备.这是个迷惑点,虽然投影矩阵包含了投影二字,但是它并没有进行真正的投影工作,而是在为投影做准备.真正的投影发生在后面的齐次排除法(homogeneous division)过程中.而经过投影矩阵变换后,顶点的w分量将会具有特殊意义.
  • 其次是对x,y,z分量进行缩放.经过投影矩阵的缩放以后,我们可以直接使用w分量作为一个范围值,如x,y,z都在这个范围内,就说明该顶点位于剪裁空间内.

1.透视投影

视锥体的六个剪裁平面是由Camera组件中的参数和Game视图的横纵比共同决定的.
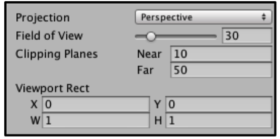
20190317193445.png
如图所示,我们可以通过Camera组件的Field of View(简称FOV)属性来改变视锥体竖直张开的角度,而Cliping Planes中的Near和Far属性可以控制视锥体的近剪裁平面和远剪裁平面距离摄像机的远近.这样,我们可以求出视锥体近剪裁平面和远剪裁平面的高度.
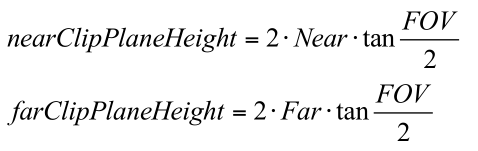
20190317193804.png
一个摄像机的横纵比由Game视图的横纵比和Viewport Rect中的W和H属性共同决定.假设,当前摄像机的横纵比是Aspect:
20190317194035.png
现在,我们可以根据已知的Near,Far,FOV和Aspect的值来确定透视投影的投影矩阵.
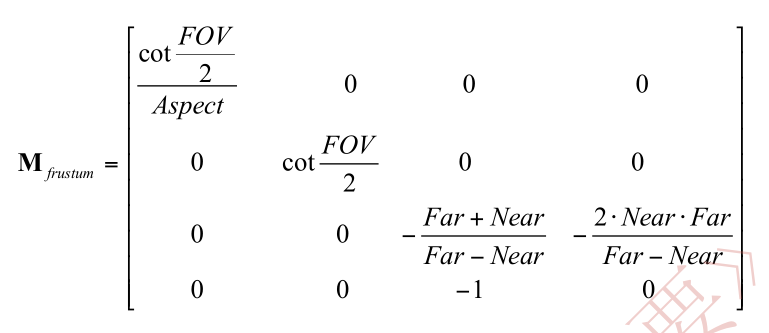
20190317194153.png
推导见本章的扩展阅读部分
一个顶点和上面的投影矩阵相乘后,可以由观察者空间变换到剪裁空间.
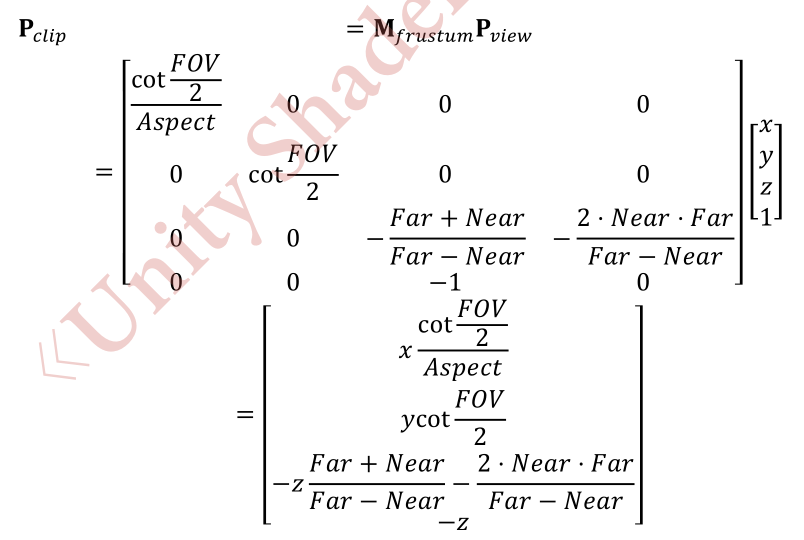
20190317194657.png
从结果可以看出来,投影矩阵的本质是对x,y,z分量做了不同的缩放(z分量还做了一个平移).缩放的目的是为了方便裁剪.
可以注意到,此时顶点的w分量不再是1,而是原先z分量的取反.现在,我们就可以按如下不等式判断一个变换后的顶点是否位于视锥体内.如果一个顶点在视锥体内,那么它变换后的坐标必须满足:

-w <= x <= w
-w <= y <= w
-w <= z <= w

任何不满足上述条件的图元都需要被剔除或者裁剪.
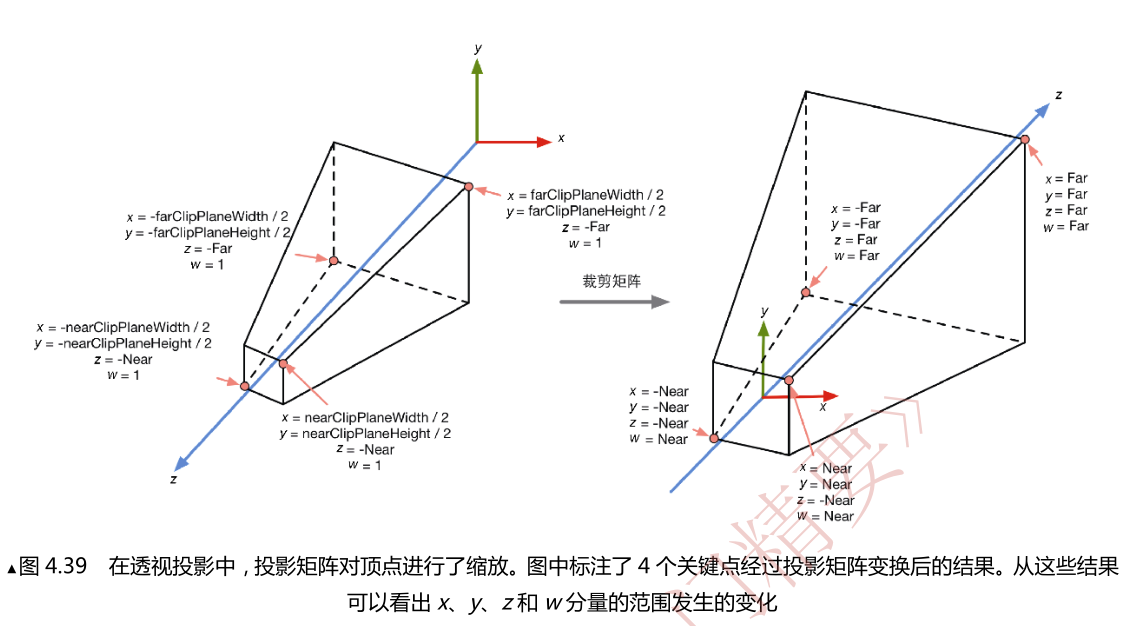
20190317195140.png
通过此图还可以注意到,剪裁矩阵会改变空间的旋向性:空间从右手坐标系变换到了左手坐标系.

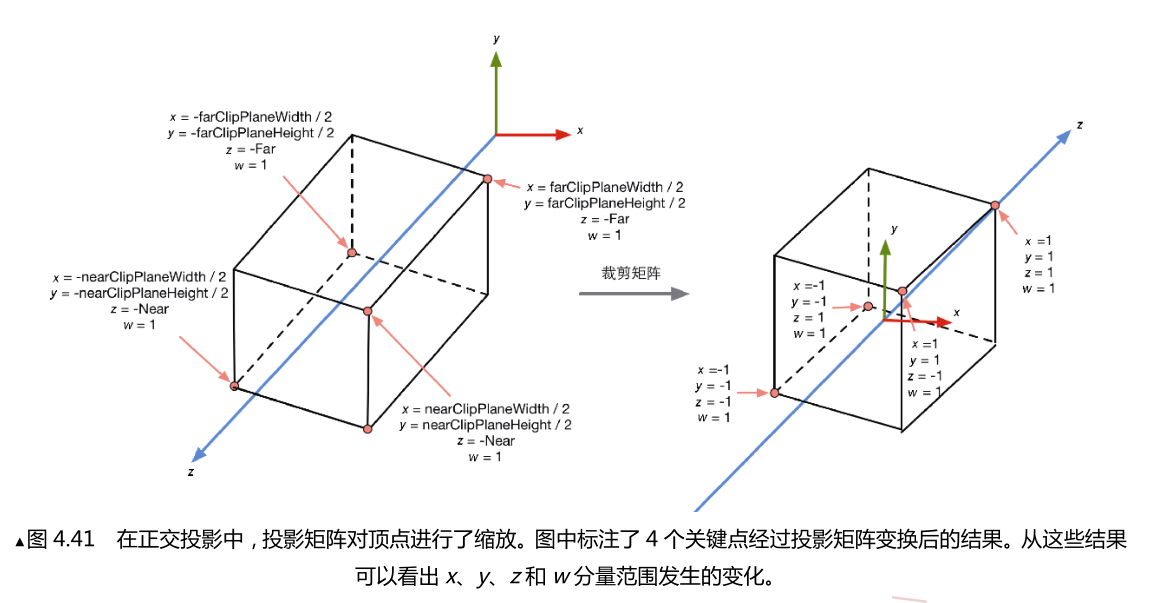
2. 正交投影

和透视投影类似,在unity中,正交投影的六个人裁剪平面是由Camera组件中的参数和Game视图的横纵比共同决定的.
20190317195733.png
由图看出,我们可以通过Camera组件的Size属性来改变视锥体竖直方向上的高度的一半,而Clipping Planes中的Near和Far参数可以控制视锥体的近剪裁平面和远剪裁平面距离摄像机的远近.这样,我们可以求出视锥体近剪裁平面和远剪裁平面的高度.即:
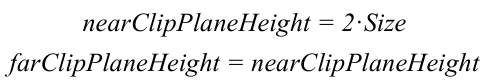
20190317200115.png
同样,我们可以通过摄像机的横纵比得到横向信息.假设当前摄像机的横纵比为Aspect:
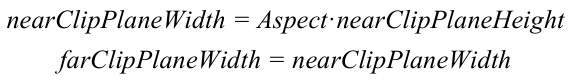
20190317222215.png

现在我们根据已知的Near,Far,Size和Aspect的值来确定正交投影的裁剪矩阵.如下:
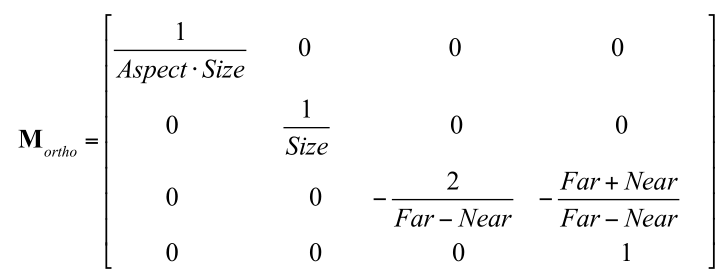
20190317222356.png
推导见本章的扩展阅读
一个顶点和上述投影矩阵相乘后的结果如下:
20190317222609.png
注意到,和透视投影不同,使用正交投影的投影矩阵对顶点变换后,其分量w依然为1.本质是因为投影矩阵最后一行的不同,透视投影的投影矩阵的最后一行是[0 0 -1 0],而正交投影的投影矩阵最后一行是[0 0 0 1].这样选择是为了为齐次除法做准备(具体在下面讲到)

判断一个变换后的顶点是否位于视锥体内使用的不等式和透视投影的一样.

同样,裁剪矩阵改变了空间的旋向性.可以注意到,经过正交投影变换后的顶点实际已经位于一个立方体内了.
20190317223446.png

屏幕空间

经过了投影矩阵的变换后,我们可以进行剪裁工作.当完成了所有的剪裁工作后,就需要进行真正的投影了.也就是说,我们需要把视锥体投影到屏幕空间(screen space)中.经过这一步变换,我们会得到真正的像素位置,二非虚拟的三维坐标.

屏幕空间是一个二维空间,因此我们需要把顶点从剪裁空间投影到屏幕空间,来生成对应的2D坐标.这个过程分为两个步骤

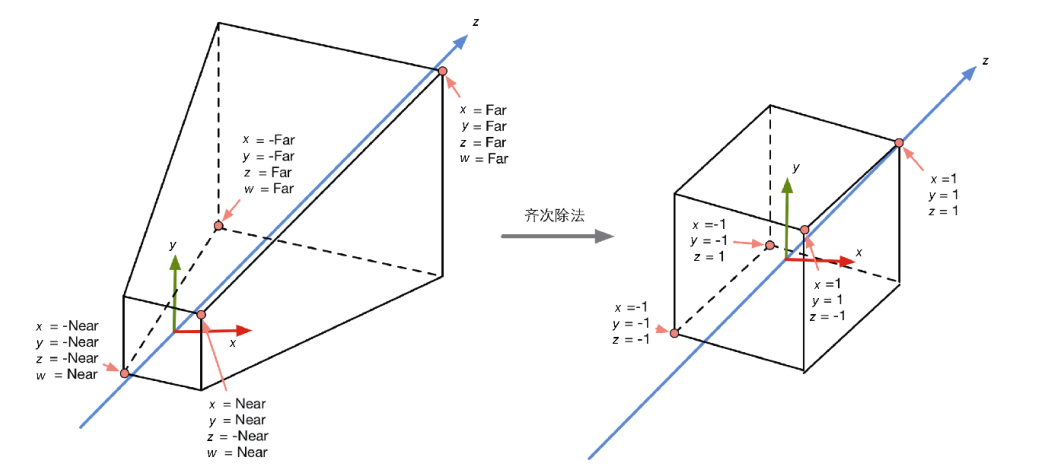
  • 首先,我们要进行标准齐次除法(homogeneous division),也被称为透视除法(perspective division).虽然这个步骤听起来陌生,但它实际上非常简单,就是用齐次坐标系的w分量去除以x,y,z分量.在OpenGL中,我们把这一步得到的坐标叫做归一化的设备坐标(Normalized Device Coordinate, NDC).经过这一步,我们可以把坐标从齐次剪裁坐标空间转换到NDC中.经过透视投影变换后的剪裁空间,经过齐次除法后会变换到一个立方体内.
对于透视投影 对于正交投影
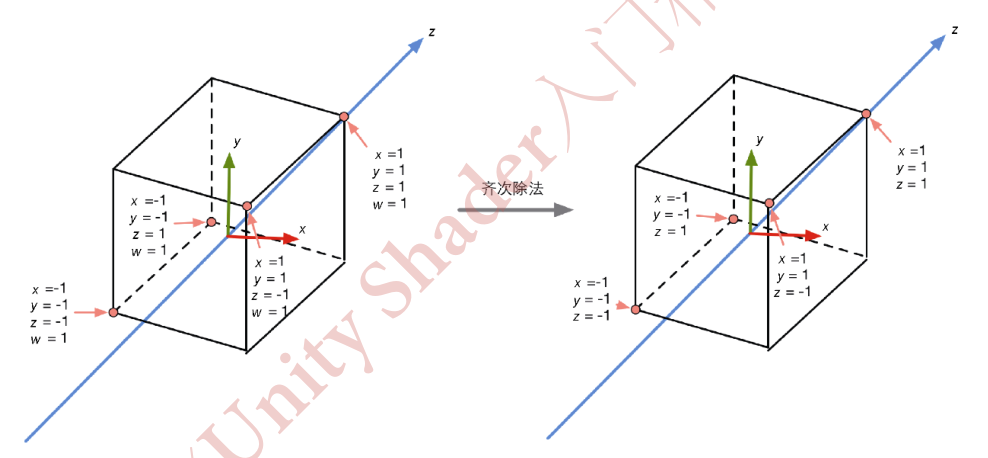20190317225205.png 20190317225220.png
经过齐次除法后,透视投影的剪裁空间会变换到一个立方体 对于正交投影来说,它的剪裁空间实际已经是一个立方体了,而且由于经过正交投影矩阵变换后的顶点的w分量是1,因此齐次除法并不会对顶点的x,y,z坐标产生影响

经过齐次除法后,透视投影和正交投影的视锥体都变换到一个相同的立方体内.现在,我们可以根据变换后的x,y坐标来映射输出窗口的对应像素坐标.
这个映射的过程是一个缩放的过程.
齐次除法和屏幕映射的过程可以用下面的公式总结:
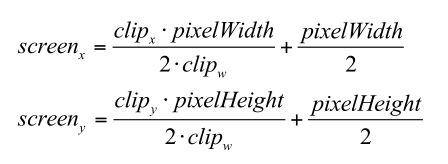
20190317225735.png
上面式子对x和y分量进行了处理,而z分量会被用于深度缓冲.一个传统的方式是把clip z / clip w的值直接存进深度缓冲中,但这不是必须的.通常驱动的生产商会根据硬件来选择最好的存储格式.
此时clip w也并未抛弃,虽然它已经完成了它的主要工作–在齐次除法中作为分母来得到NDC,但它仍然会在后续的一些工作中起到重要作用.例如进行透视矫正差值(这又是什么玩意)

在Unity中,从剪裁空间到屏幕空间的转换是底层帮我们完成的.我们的顶点着色器只需要把顶点转换到剪裁空间即可.

总结

以上就是一个顶点如何从模型空间最终转换到屏幕空间的全过程.
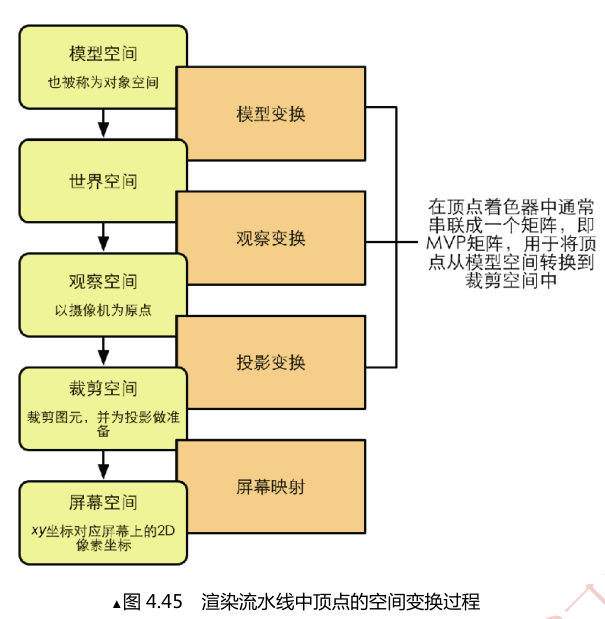
20190317230752.png

顶点着色器的最基本的任务是把顶点坐标从模型空间转换到剪裁空间中.这对应了上图中的前三个顶点变换过程.而在片元着色器中,我们通常也可以得到该片元在屏幕空间的像素信息.我们会在4.9.3节中看到如何得到这些像素位置.

在Unity中,坐标系的旋向性也随着发生了改变.
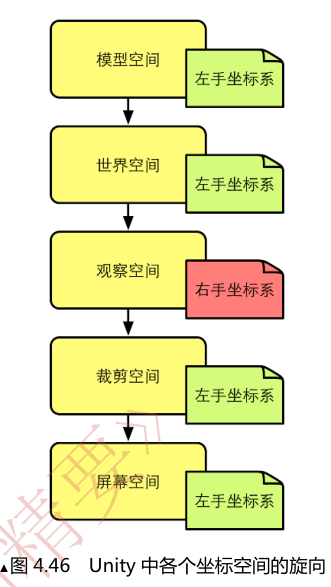
20190317231135.png
只有在观察空间使用了右手坐标系.

需要注意的是,这里仅仅给出的是一些最重要的坐标空间.还有一些空间在实际开发中也会遇到,如切线空间(tangent space).切线空间通常用于法线映射.

法线变换

法线(normal),也被称为法矢量(normal vector).
在游戏中,模型的一个顶点往往会携带额外的信息,而顶点法线就是其中的一种信息.
当我们变换一个模型的时候,不仅要变换它的顶点,还需要变换它的法线,以便在后续的处理(如片元着色器)中计算光照等.
这块数学公式太多了md不要表达,反正本来的这块内容就没多少去书上看吧.

Unity Shader的内置变量(数学篇)

变换矩阵

这里是Unity5.2版本提供的所有内置变换矩阵.所有矩阵都是float4x4的.

变量名 描述
_Object2World 当前的模型矩阵,用于将顶点/方向矢量从模型空间变换到世界空间
_World2Object _Object2World的逆矩阵.用于将顶点/方向矢量从世界空间变换到模型空间
UNITY_MATRIX_V 当前的观察矩阵,用于将顶点/方向矢量从世界空间变换到观察空间
UNITY_MATRIX_P 当前的投影矩阵,用于将顶点/方向矢量从观察空间变换到剪裁空间
UNITY_MATRIX_MV 当前的模型矩阵·观察矩阵,用于将顶点/方向矢量从模型空间变换到观察空间
UNITY_MATRIX_VP 当前的观察矩阵·投影矩阵,用于将顶点/方向矢量从世界空间转换到剪裁空间
UNITY_MATRIX_MVP 当前的模型矩阵·观察矩阵·投影矩阵,用于将顶点/方向矢量从模型空间变换到剪裁空间
UNITY_MATRIX_T_MV UNITY_MATRIX_MV的转置矩阵
UNITY_MATRIX_IT_MV UNITY_MATRIX_MV的逆转置矩阵,用于将法线从模型空间变换到世界观察空间,也可用于得到UNITY_MATRIX_MV的逆矩阵

UNITY_MATRIX_T_MV这个矩阵比较特殊.
对于正交矩阵来说,它的逆矩阵就是转置矩阵.因此,如果UNITY_MATRIX_MV是一个正交矩阵的话,那么UNITY_MATRIX_T_MV就是它的逆矩阵,也就是说,我们可以使用UNITY_MATRIX_T_MV将顶点/方向矢量从观察空间变换到模型空间

UNITY_MATRIX_IT_MV这个矩阵也要特殊说明一下.
法线的变换需要使用原变换矩阵的逆转矩阵,因此UNITY_MATRIX_IT_MV可以把发现从模型空间变换到观察者空间.而且,只需要对它进行转置,就可以得到UNITY_MATRIX_MV的逆矩阵因此,为了把顶点或法线矢量从观察者空间变换到模型空间,我们可以使用以下代码:

1
2
3
4
5
// 方法一: 使用transpose函数对UNITY_MATRIX_IT_MV进行转置,得到UNITY_MATRIX_MV的逆矩阵,然后进行列矩阵乘法,把观察空间中的点或方向矢量变换到模型空间中  
float4 modelPos = mul(transpose(UNITY_MATRIX_IT_MV), viewPos);

// 方法二: 不直接使用转置函数transpose, 而是交换mul参数的位置,使用行矩阵乘法. 本质是一样的.
float4 modelPos = mul(viewPos, UNITY_MATRIX_IT_MV);

摄像机和屏幕参数

Unity提供了一些内置变量来让我们访问当前正在渲染的摄像机的参数信息.这些参数对应了摄像机上的Camera组件中的属性值.

变量名 类型 描述
_WorldSpaceCameraPos float3 该摄像机在世界空间中的位置
_ProjectionParams float4 x = 1.0(或-1.0, 如果正在使用一个翻转的投影矩阵进行渲染), y = Near, z = Far, w = 1.0 + 1.0/Far
_ScreenParams float4 x = wodth, y = height, z = 1.0 + 1.0/width, w = 1.0 + 1.0/height
_ZBufferParams float4 x = 1 - Far/Near, y = Far/Near, z = x/Far, w = y/Far, 该变量用于线性化Z缓存中的深度值(可参考13.1节)
unity_OrthoParams float4 x = width, y = height,z没有定义,w = 1.0(该摄像机是正交摄像机),或w = 0.0(该摄像机是透视摄像机)
unity_CameraProjectio float4x4 该摄像机的投影矩阵
unity_CameraInvProjection float4x4 该摄像机的投影矩阵的逆矩阵
unity_CameraWorldClipPlanes[6] float4 该摄像机的6个裁剪平面在世界空间下是等式.按如下顺序:左,右,下,上,近,远裁剪平面